Frank Schäfer

Postdoctoral researcher

Julia Lab @ MIT

Biography

I am a postdoc in the Julia Lab located in the Computer Science and Artificial Intelligence Laboratory (CSAIL) at the Massachusetts Institute of Technology (MIT). My research is focused on Scientific Machine Learning (SciML). I completed my PhD in physics in the Bruder group within the “Quantum Computing and Quantum Technology” PhD school at the University of Basel. During my PhD, I participated in the Google Summer of Code (GSoC) 2020 and 2021 programs with the projects “High weak order stochastic differential equation solvers and their utility in neural stochastic differential equations” within the Julia Language organization and “Neural Hybrid Differential Equations and Adjoint Sensitivity Analysis” within the NumFocus organization, supervised by Chris Rackauckas, Moritz Schauer, Mohamed Tarek, and Yingbo Ma. Since 2020, I am a member of the SciML open source software organization for scientific machine learning.

Interests

Probabilistic machine learning
Differentiable & probabilistic programming
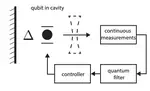
Quantum & stochastic optimal control
Parameter inference / estimation theory
Stochastic processes and many-body physics

Education

PhD in Physics under the supervision of Prof. Dr. Christoph Bruder, 2022

Department of Physics, University of Basel
MSc in Physics under the supervision of Prof. Dr. Andreas Buchleitner, 2018

Department of Physics, Albert-Ludwigs-Universität Freiburg
BSc in Physics under the supervision of PD Dr. Thomas Wellens, 2015

Department of Physics, Albert-Ludwigs-Universität Freiburg

Posts

Neural Hybrid Differential Equations and Adjoint Sensitivity Analysis

Project summary In this project, we have implemented state-of-the-art sensitivity tools for chaotic dynamical systems, continuous adjoint sensitivity methods for hybrid differential equations, as well as a high level API for automatic differentiation.

Aug 13, 2021 3 min read

AbstractDifferentiation.jl for AD-backend agnostic code

Differentiable programming (∂P), i.e., the ability to differentiate general computer program structures, has enabled the efficient combination of existing packages for scientific computation and machine learning1. The Julia2 language is well suited for ∂P, see also Chris’ article3 for a detailed examination.

Aug 1, 2021 11 min read

Sensitivity Analysis of Hybrid Differential Equations

In this post, we discuss sensitivity analysis of differential equations with state changes caused by events triggered at defined moments, for example reflections, bounces off a wall or other sudden forces.

Frank Schäfer and Moritz Schauer

Jul 16, 2021 19 min read

Shadowing Methods for Forward and Adjoint Sensitivity Analysis of Chaotic Systems

In this post, we dig into sensitivity analysis of chaotic systems. Chaotic systems are dynamical, deterministic systems that are extremely sensitive to small changes in the initial state or the system parameters.

Jul 2, 2021 9 min read

Neural Hybrid Differential Equations

I am delighted that I have been awarded my second GSoC stipend this year. I look forward to carrying out the ambitious project scope with my mentors Chris Rackauckas, Moritz Schauer, Yingbo Ma, and Mohamed Tarek.

Jun 16, 2021 7 min read

See all posts

Research projects

Automatic Differentiation of Programs with Discrete Randomness

We develop and implement AD algorithms for handling programs that can contain discrete randomness.

FS in Collaboration With Gaurav Arya, Moritz Schauer, Ruben Seyer, Alex Lew, Mathieu Huot, Kartik Chandra, Vikash Mansinghka, Jonathan Ragan-Kelley, Chris Rackauckas

Automatic Differentiation of Programs with Discrete Randomness

Performance Bounds for Quantum Control

We compute bounds for the best attainable control performance that may serve as certificates of fundamental limitations or performance targets.

FS in Collaboration With Flemming Holtorf, Julian Arnold, Chris Rackauckas, And Alan Edelman

Control of (Stochastic) Quantum Dynamics with Differentiable Programming

Quantum control based on parametrized controllers trained with gradient information computed by (adjoint) sensitivity methods.

FS in Collaboration With Pavel Sekatski, Martin Koppenhöfer, Niels Lörch, Christoph Bruder, And Michal Kloc

Control of (Stochastic) Quantum Dynamics with Differentiable Programming

Automated Data-driven Reconstruction of Physical Properties

We address the challenges of connecting measurements of a physical system to an underlying theoretical description.

FS in Collaboration With Eliska Greplova, Tomoki Hirosawa, Jozef Bucko, František Herman, Rebekka Garreis, Chuyao Tong, Annika Kurzmann, Thomas Ihn, Hideaki Maebashi, Hiroyasu Matsuura, And Masao Ogata

Automated Data-driven Reconstruction of Physical Properties

Machine Learning for Phase Transitions

Data-driven methods based on sample instances of the state of a physical system as a function of the system’s parameters.

FS in Collaboration With Julian Arnold, Flemming Holtorf, Eliska Greplova, Agnes Valenti, Martin Zonda, Axel Lode, Gregor Boschung, Sebastian Huber, And Niels Lörch