Control of (Stochastic) Quantum Dynamics with Differentiable Programming

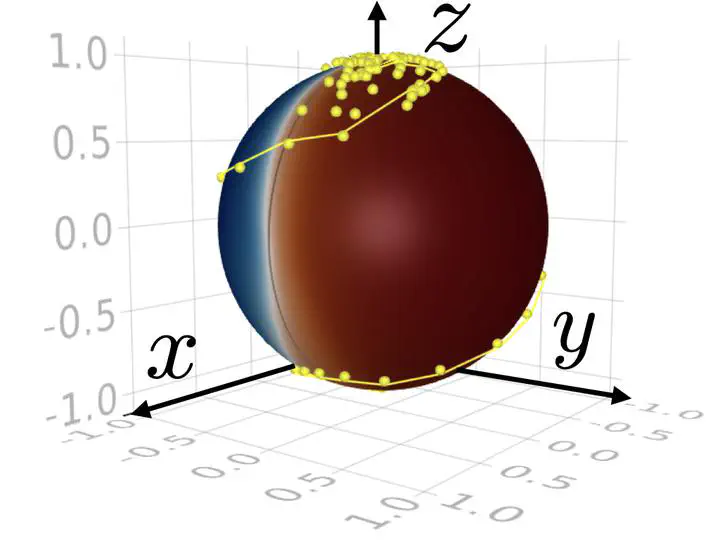
Conceptually, it is straightforward to determine the time evolution of a quantum system for a fixed initial state given its (time-dependent) Hamiltonian or Lindbladian. Depending on the physical context, the dynamics is described by an ordinary or stochastic differential equation. In quantum state control, which is of paramount importance for quantum computation, we aim at solving the inverse problem. That is, starting from a distribution of initial states, we seek protocols that allow us to reach a desired target state by optimization of free parameters of the differential equation (control drives) in a certain time interval. To solve this control problem, we implement the system dynamics as part of a fully differentiable program and use a loss function that quantifies the distance from the target state. Specifically, we employ a neural network that maps an observation of the state of the qubit to a control drive defined via the differential equation for each time interval. To implement efficient training, we backpropagate the gradient information from the loss function through the SDE solver using adjoint sensitivity methods. Such a procedure should ultimately combine powerful tools from machine learning and scientific computation.