Performance Bounds for Quantum Control

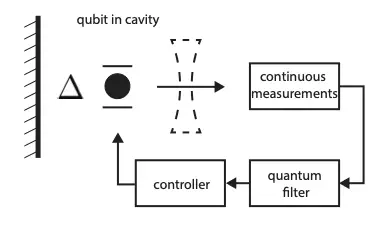
Control of devices at the quantum level holds enormous potential for current and future applications in the field of quantum information science. However, due to the nonlinear and stochastic nature of quantum systems under continuous observation, analytical solutions to all but the simplest quantum control problems remain unknown. In this project, we present a convex optimization framework to compute informative bounds on the best attainable control performance. Since our approach provides an under-approximator for the value function, we can use it directly to construct near-optimal heuristic controllers as demonstrated for a qubit subjected to homodyne detection and photon counting.