GSoC 2020: High weak order SDE solvers and their utility in neural SDEs

First and foremost, I would like to thank my mentors Chris Rackauckas, Moritz Schauer, and Yingbo Ma for their willingness to supervise me in this Google Summer of Code project. Although we are still at the very beginning of the project, we already had plenty of very inspiring discussion. I will spend the following months implementing both new high weak order solvers as well as adjoint sensitivity methods for stochastic differential equations (SDEs). The project is embedded within the SciML organization which, among others, unifies the latest toolsets from scientific machine learning and differential equation solver software. Ultimately, the planned contributions will allow researchers to simulate (or even control) stochastic dynamics. Also inverse problems, where SDE models are fit to data, fall into the scope. Therefore, relevant applications are found in many fields ranging from the simulation of (bio-)chemical processes over financial modeling to quantum mechanics.

This post is supposed to summarize what we have implemented in this first period and what we are going to do next. Future posts are going to dig into the individual subjects in more details.

High Weak Order Solvers

Currently, the StochasticDiffEq package contains state-of-the-art solvers for the strong approximation of SDEs, i.e., solvers that allow one to reconstruct correctly the numerical solution of an SDE in a pathwise sense. In general, an accurate estimation of multiple stochastic integrals is then required to produce a strong method of order greater than 1/2.

However in many situations, we are only aiming for computing an estimation for the expected value of the solution. In such situations, methods for the weak approximation are sufficient. The less restrictive formulation of the objective for weak methods has the advantage that they are computationally cheaper than strong methods. High weak order solvers are particularly appealing, as they allow for using much larger time steps while attaining the same error in the mean, as compared with SDE solvers having a smaller weak order convergence. As an example, when Monte Carlo methods are used for SDE models, it is indeed often sufficient to be able to accurately sample random trajectories of the SDE, and it is not important to accurately approximate a particular trajectory. The former is exactly what a solver with high weak order provides.

Second order Runge-Kutta methods for Ito SDEs

In the beginning of the community bonding period I finished the implementations of the DRI1()¹ and RI1()² methods. Both are representing second order Runge-Kutta schemes and were introduced by Rößler. Interestingly, these methods are designed to scale well with the number of Wiener processes m. Specifically, only 2m-1 random variables have to be drawn (in contrast to m(m+1)/2 from previous methods). Additionally, the number of function evaluations for the drift and the diffusion terms is independent of m.

As an example, we can check the second order convergence property on a multi-dimensional SDE with non-commuting noise¹:

$$ \scriptstyle d \begin{pmatrix} X_1 \\ X_2 \end{pmatrix} = \begin{pmatrix} -\frac{273}{512} & \phantom{X_2}0 \\ -\frac{1}{160} \phantom{X_2} & -\frac{785}{512}+\frac{\sqrt{2}}{8} \end{pmatrix} \begin{pmatrix} X_1 \\ X_2 \end{pmatrix} dt + \begin{pmatrix} \frac{1}{4} X_1 & \frac{1}{16} X_1 \\ \frac{1-2\sqrt{2}}{4} X_2 & \frac{1}{10}X_1 +\frac{1}{16} X_2 \end{pmatrix} d \begin{pmatrix} W_1 \\ W_2 \end{pmatrix}
$$

with initial value $$ X(t=0)= \begin{pmatrix} 1 \\ 1\end{pmatrix}.$$

For the function $f(x)=(x_1)^2$, we can analytically compute the expected value of the solution

$$ \rm{E}\left[ f(X(t)) \right] = \exp(-t),$$

which we use to test the weak convergence order of the algorithms in the following.

To compute the expected value numerically, we sample an ensemble of numtraj = 1e7 trajectories for different step sizes dt. The code for a single dt reads:

using StochasticDiffEq
numtraj = 1e7
u₀ = [1.0,1.0]
function f!(du,u,p,t)
  du[1] = -273//512*u[1]
  du[2] = -1//160*u[1]-(-785//512+sqrt(2)/8)*u[2]
end
function g!(du,u,p,t)
  du[1,1] = 1//4*u[1]
  du[1,2] = 1//16*u[1]
  du[2,1] = (1-2*sqrt(2))/4*u[1]
  du[2,2] = 1//10*u[1]+1//16*u[2]
end
dt = 1//8
tspan = (0.0,10.0)
prob = SDEProblem(f!,g!,u₀,tspan,noise_rate_prototype=zeros(2,2))

h(z) = z^2

ensemble_prob = EnsembleProblem(prob;
        output_func = (sol,i) -> (h(sol[end][1]),false)
        )
sol = solve(ensemble_prob, DRI1();
        dt=dt,
        save_start=false,
        save_everystep=false,
        weak_timeseries_errors=false,
        weak_dense_errors=false,
        trajectories=numtraj)

We then compute the error of the numerically obtained expected value of the ensemble simulation with respect to the analytical result:

LinearAlgebra.norm(Statistics.mean(sol.u)-exp(-tspan[2]))

Repeating this procedure for some more values of dt, the log-log plot of the error as a function of dt displays nicely the second order convergence (slope $\approx 2.2$).

In the next couple of weeks, my focus will be on

• adding other high weak order solvers,
• implementing adaptive time stepping.

More of our near-term goals are collected in this issue.

Adjoint Sensitivity Methods for SDEs

In parameter estimation/inverse problems, one is interested to know the optimal choice of parameters p such that a model f(p), e.g., a differential equation, optimally fits some data, y. The shooting method approaches this task by introducing some sort of loss function $L$. A common choice is the mean squared error

$$ L = |f(p)-y|^2. $$

An optimizer is then used to update the parameters $p$ such that $L$ is minimized. For this fit, local optimizers use the gradient $\frac{dL}{dp}$ to minimize the loss function and ultimately solve the inverse problem. One possibility to obtain the gradient information for (stochastic) differential equations is to use automatic differentiation (AD). While forward mode AD is memory efficient, it scales poorly in time with increasing number of parameters. On the contrary, reverse-mode AD, i.e., a direct backpropagation through the solver, has a huge memory footprint.

Alternatively to the “direct” AD approaches, the adjoint sensitivity method can be used³. The adjoint sensitivity method is well known to compute gradients of solutions to ordinary differential equations (ODEs) with respect to the parameters and initial states entering the ODE. The method was recently generalized to SDEs⁴. Importantly, this new approach has different complexities in terms of memory consumption or computation time as compared with forward- or reverse-mode AD (NP vs N+P where N is the number of state variables and P is the number of parameters).

It turns out that the aforementioned gradients in the stochastic adjoint sensitivity method are given by solving an SDE with an augmented state backwards in time launched at the end state of the forward evolution. In other words, we first compute the forward time evolution of the model from the start time $t_0$ to the end time $t_1$. Subsequently, we reverse the SDE and run a second time evolution from $t_1$ to $t_0$. Please note that the authors in Ref. ⁴ are implementing a slightly modfified version where the time evolution of the augmented state runs from $-t_1$ to $-t_0$. We however are indeed using the former variant as it allows us to reuse/generalize many functions that were implemented in the DiffEqSensitivity package for ODE adjoints earlier.

Reverse SDE time evolution

The reversion of an SDE is more difficult than the reversion of an ODE. However, for SDEs written in the Stratonovich sense, it turns out that reversion can be achieved by negative signs in front of the drift and diffusion terms. As one needs to follow the same trajectory backward, the noise sampled in the forward pass must be reconstructed. In general, we would like to use adaptive time-stepping solvers which require some form of interpolation for the noise values. After some fixes for the available noise processes, we are now able to reverse a stochastic time evolution either by using NoiseGrid which linearly interpolates between values of the noise on a given grid or by using a very general NoiseWrapper which interpolates in a distributionally-exact manner based on Brownian bridges.

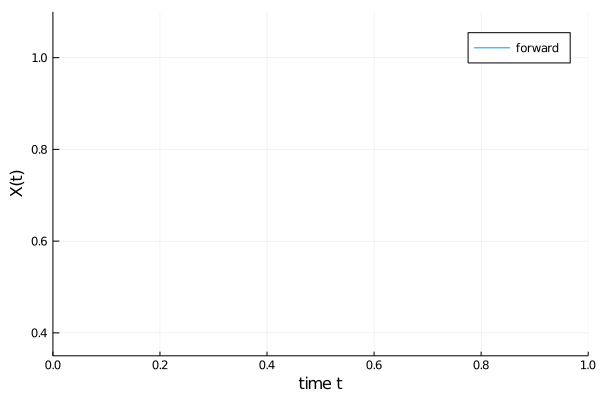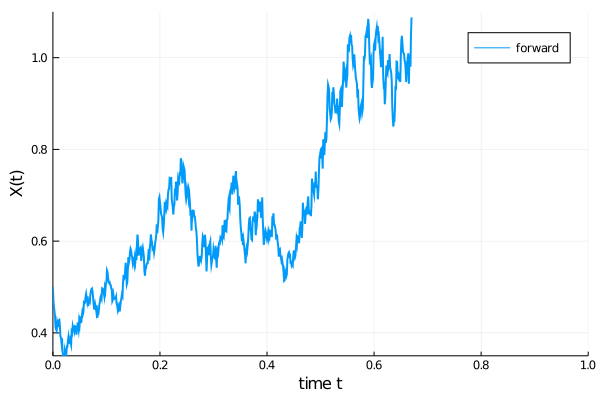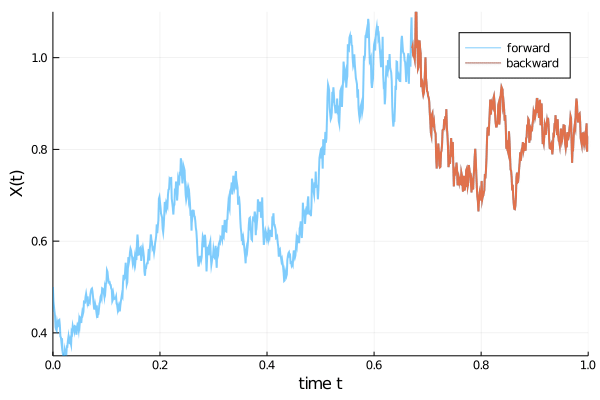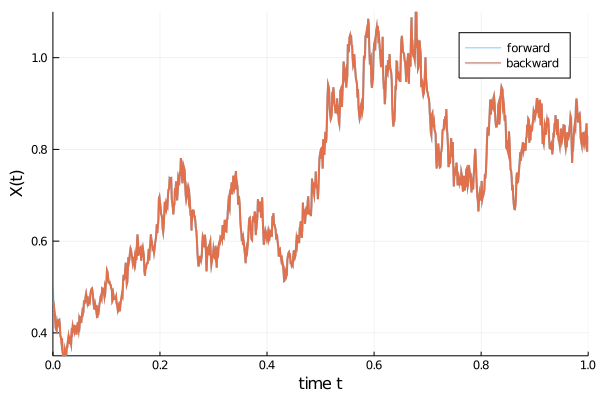
As an example, the code below computes first the forward evolution of an SDE

$$ dX = \alpha X dt + \beta X dW$$

with $\alpha=1.01$, $\beta=0.87$, $x(0)=1/2$, in the time span ($t_{0}=0$, $t_{1}=1)$. This forward evolution is shown in blue in the animation below. Subsequently, also the reverse time evolution (red) launched at time $t_{1}=1$ with initial value $x(t=1)$, propagated in negative time direction until $t_{0}=0$, is computed. We see that both trajectories match very well.

  using StochasticDiffEq, DiffEqNoiseProcess

  α=1.01
  β=0.87

  dt = 1e-3
  tspan = (0.0,1.0)
  u₀=1/2

  tarray =  collect(tspan[1]:dt:tspan[2])

  f!(du,u,p,t) = du .= α*u
  g!(du,u,p,t) = du .= β*u


  prob = SDEProblem(f!,g!,[u₀],tspan)
  sol =solve(prob,EulerHeun(),dt=dt,save_noise=true, adaptive=false)

  _sol = deepcopy(sol) # to make sure the plot is correct
  W1 = NoiseGrid(reverse!(_sol.t),reverse!(_sol.W.W))
  prob1 = SDEProblem(f!,g!,sol[end],reverse(tspan),noise=W1)
  sol1 = solve(prob1,EulerHeun(),dt=dt)

Gradients of diagonal SDEs

I have already started to implement the stochastic adjoint sensitivity method for SDEs possessing diagonal noise. Currently, only out-of-place SDE functions are supported but I am optimistic that soon also the inplace formulation works.

Let us consider again the linear SDE with multiplicative noise from above (with the same parameters). This SDE represents one of the few exact solvable cases. In the Stratonovich sense, the solution is given as

$$ X(t) = X(0) \exp(\alpha t + \beta W(t)).$$

We might be interested in optimizing the parameters $\alpha$ and $\beta$ to minimize a certain loss function acting on the solution $X(t)$. For such an optimization task, a useful search direction is indicated by the gradient of the loss function with respect to the parameters. The latter however requires the differentiation through the SDE solver – if no analytical solution of the SDE is available.

As an example, let us consider a mean squared error loss

$$ L(X(t)) = \sum_i |X(t_i)|^2, $$

acting on the solution $X(t)$ for some fixed time points $t_i$. Then, the analytical forms for the gradients here read

$$ \begin{aligned} \frac{d L}{d \alpha} &= 2 \sum_i t_i |X(t_i)|^2 \\ \frac{d L}{d \beta} &= 2 \sum_i W(t_i) |X(t_i)|^2 \end{aligned} $$

for $\alpha$ and $\beta$, respectively. We can confirm that this agrees with the gradients as obtained by the stochastic adjoint sensitivity method

using Test, LinearAlgebra
using DiffEqSensitivity, StochasticDiffEq
using Random

seed = 100
Random.seed!(seed)

u₀ = [0.5]
tstart = 0.0
tend = 0.1
dt = 0.005
trange = (tstart, tend)
t = tstart:dt:tend
tarray = collect(t)

function g(u,p,t)
  sum(u.^2.0)
end

function dg!(out,u,p,t,i)
  (out.=-2.0*u)
end

p2 = [1.01,0.87]

f(u,p,t) = p[1]*u
σ(u,p,t) = p[2]*u


Random.seed!(seed)
prob = SDEProblem(f,σ,u₀,trange,p2)
sol = solve(prob,RKMil(interpretation=:Stratonovich),dt=tend/1e7,adaptive=false,save_noise=true)
res_u0, res_p = adjoint_sensitivities(sol,EulerHeun(),dg!,t,dt=tend/1e7,sensealg=BacksolveAdjoint())


noise = vec((@. sol.W(tarray)))
Wextracted = [W[1][1] for W in noise]
resp1 = 2*sum(@. tarray*u₀^2*exp(2*(p2[1])*tarray+2*p2[2]*Wextracted))
resp2 = 2*sum(@. Wextracted*u₀^2*exp(2*(p2[1])*tarray+2*p2[2]*Wextracted))
resp = [resp1, resp2]

@test isapprox(res_p', resp, rtol = 1e-6)
# True

With respect to the adjoint sensitivity methods, we are planning to

• finish the current backsolve adjoint version,
• allow for computing the gradients of non-commuting SDEs,
• implement also an interpolation adjoint version,
• benchmark it with respect to AD approaches

in the upcoming weeks. For more information, the interested reader might take a look at the open issues in the DiffEqSensitivity package.

If you have any questions or comments, please don’t hesitate to contact me!